Fun Science / Another Aspect of Reality
After thousands of requests I got from my readers around the world, I will try to explain one of the darkest corners of Quantum Mechanics: The EPR paradox, Bell’s inequalities, the Aspect experiment, reality and locality in Quantum Mechanics (QM).
The story consists of 2 parts. First, the original EPR paradox stated by Einstein, Podolsky and Rosen in 1935, where they argued that QM is not complete as a theory. Second, Bell formulated some inequalities that relate to the paradox and they can be experimentally tested. Aspect in 1983 performed the experiment and proved that Einstein was wrong, and that Bell’s inequality is violated.
The EPR Paradox
Usually when people try to explain physics, they come up with a real world example, an analogy that non-scientists can grasp, in order to make themselves understood. Although I do not completely agree with the approach, since it reduces the complexity by taking away critical facts, I will use an example here which is ok as long as one realizes the restrictions that apply.
In their EPR paper Einstein, Podolsky and Rosen proposed a thought experiment that goes something like that. Imagine you and a friend are magically given each a piece of paper and that each paper has inscribed a positive integer on it, and you are told that the numbers on each paper is random, under the condition that their product is always 24. Then you drive to the east coast, and your friend drives to the west coast.
When you read the paper, say the number 12, you instantly know that the number written in the other paper is 2. Similarly, if you repeat the experiment and you finally read 6, you instantly know that your friend’s paper reads 4, etc.
The point here is to realize that the 2 properties (the numbers) are random yet they have to satisfy some combining condition that you know ahead of time. This is ok as long as the numbers are predetermined and written on the papers beforehand.
However, the problem arises because Quantum Mechanics says that the number you read is determined at the exact moment you read the paper (i.e, after you travel to the east coast). Hence at the same moment the other number on the other coast is determined afterwards and at the same time you conduct your experiment, i.e. when you read the paper. This means that a faster than light signal (forbidden by relativity) is somehow transmitted from one side to the other. This is the EPR paradox.
In their paper they attempted to resolve the paradox by introducing the so called hidden variables; that despite what QM says, there are some hidden variables that pre-determine the value of the numbers at their origin point. Bell later on derived an inequality that expresses exactly this fact. And Aspect proved that it was all wrong.
Here we must distinguish between causality and locality. Causality means that something is happening before its cause (e.g. faster than light speed); locality means that there is a “spooky action at a distance” that allows something to be affected instantly by something on the other side of the universe. The experiment proved that Quantum Mechanics violates locality but not causality.
In reality, instead of numbers in pieces of paper people use photons with polarizations (the direction that the vector is pointing). What they do is they generate e.g. photons that must have opposite polarizations, so if one is up the other has to be down and vice versa. However the initial state of the photon is random, it can be either. And EPR say the state is determined in the birth of the photons, while QM says it is determined at the instant of observation of either photon.
So, it remains to be seen how the experiment proved how QM was right after all.
A Simple Experiment
Bell’s inequalities are infinite in number since they depend on the experimental setup and the type of questions we ask about the system. Here is the version that I am going to use:
Probability of getting the same color from both detectors >= 5/9
So I will setup an experiment for which the above inequality makes sense. I will prove that using common sense and locality, the inequality is satisfied. Then I will use some simple Quantum Mechanics and defy locality to prove that the inequality is violated (in fact I will prove the probability to be 1/2). And I will do that using only high school math.
In 1983 Aspect did the corresponding experiment and found that the inequality is indeed violated, confirming that QM is a non local theory (i.e. there are no hidden variables and there is an instant communication between 2 photons).
Here are the rules:
-
We have a source that emits a pair of 2 identical photons. Each pair may have different properties, but the photons inside each pair are identical. Each photons heads towards a different detector.
-
We have 2 detectors that can flash either red or green, depending on the polarization (direction) of the photons.
-
Each detector can be aligned randomly along one of 3 predetermined axes of polarization. Let’s assume for example that these axes are at 120 degrees angle with eachother. We name these positions 1, 2 and 3. Each detector can be set independent from the other.
-
The photon source emits 2 types of pairs of photons, type I and type II. We cannot know which type of pair is emitted at each take of the experiment.
-
Type I pairs of photons always cause both detectors two flash green (for example, the photons can have polarization that is never opposite to any of the 3 main axes - they will always contain some component in any of the 3 axes; hence it doesn’t matter how the detectors are aligned, they will always both flash green). The probability of the detectors flashing the same color is 1.
-
Type II pairs of photons cause the detectors to flash green only when the detector is oriented at position 2 (the polarization of the photon is along that direction). Then each detector will flash green exactly 1/3 of the time. What is the probability that both detectors will flash the same color? You can prove simply that this is 5/9:
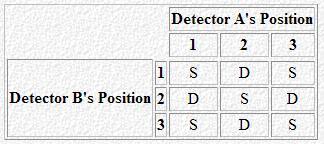
So, whenever any detector is set at position 2 and the other one isn’t then they flash a different color (D) ; in any other case they flash the same (S). Take some time to convince yourselves for that since this is the whole proof!
Now, Bell’s inequality comes as an answer to the question: What is the probability of getting the same color from both detectors? Answer: the probability is always equal or greater than 5/9. In our case this probability is either 5/9 (if type II photons are emitted) or 1 (if type I photons are emitted).
Probability of getting the same color from both detectors >= 5/9
This is the common sense answer and it seems like there can be nothing else other than that. That is because you implicitly assume that the property of each pair of photons (whether it is type I or II) is pre-determined at the birth of the photons. However in the next part I will prove that QM allows for the probability to be 1/2, which means that the determination of the type happens exactly when the detector flashes, and not beforehand!
Here we will conclude the treatment of the violation of Bell’s inequality.
Recall that we have an experiment where 2 photons are generated with a certain (identical to each other but different from shot to shot) polarization and fly in opposite directions. At the end of their trip we set up two detectors, A and B, which can be oriented at random in any of 3 predetermined axes 1,2,3 in order to measure the polarization of the photons.
We need to calculate the probability that both detectors will flash the same color, which according to Bell’s inequality (from part 2) is 5/9.the detectors flash green when they detect something along the direction they are aligned, and red if they don’t.
Here we will use Quantum Mechanics to prove that the probability is 1/2. We will need only 3 facts here, all of which are a consequence of QM:
-
The polarization in each photon is decided only when we measure them. Let me explain, since this is the most crucial difference: Until we measure any of the photons, we do not have any clue as to what their polarization is. In fact, the polarization is not determined until we make the measurement (hence it is not decided at the birth but only when we measure them). Also, since (as before in part 2) the photons are born correlated (identical) once we find out the polarization in one of them the other one will instantly acquire (at that exact moment!) the same polarization.
This is the spooky action at a distance that Einstein objected to. The main difference with part 2 is that the polarization is not decided at birth but the measurement itself specifies it. -
Collapse of the wavefunction. This is a standard result of QM (Einstein was ok with that). When you make a measurement and find the polarization along a certain direction, subsequent measurements will always yield the same result with probability 1. This is because once you measure something, there is no uncertainty thereafter as to what the value is. For example, if a detector is along direction 3 and it flashes green, then any other measurement will find the same photon to be along direction 3.
Here is the critical step though: In addition, from assumption 1, the other photon will instantly be forced to have polarization along direction 3 too, even though we measured the first photon! Hence not only the measured photon will always yield again the same result with probability 1, but the other photon (due to the correlation they had from birth) will always yield the same result with probability 1 also…
At this point you should go back and read the last paragraph again since here lies the difference between the classical common sense description and the Quantum Mechanical one. In QM the measurement of the first photon will INSTANTLY force BOTH photons to align in the same direction, which is the direction of the axis of the detector. In the classic view this does not happen since the direction of the photons is predetermined at birth and it is fixed since then. Keep also in mind that the direction of the axis of the detectors is decided right before the photons hits the detector, while the other photon is far far away.
For example, we decide to put the detector along direction 1 and then we get a green light from photon A, which means that photon B is instantly also aligned with along direction 1. Then in the next shot we decide to put the detector along direction 2, and we get a red light from photon A, which means that photon B is instantly aligned opposite of direction 2 (same with photon A). -
If the polarization of a photon forms an angle θ with respect to the orientation detector, the probability that the detector will flash green is P=cos^2(θ/2). This is a Quantum Mechanical result that I will not prove here, but I will explain how it makes a lot of sense to be that way.
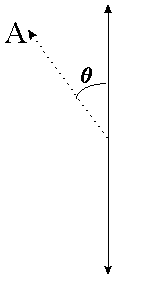
Here, the photon is pointing up and the detector is along some direction A that forms and angle θ with the polarization of the photon. First, observe that cos^2(θ/2) is always positive and between 0 and 1 (like any probability!). Second, for θ=0 the detector is exactly along the polarization of the photon and hence it will always flash green (P=1). Third, for θ=180 degrees the detector is aligned opposite of the polarization and hence it will always flash red (P=0). Fourth, for θ=90 degrees, the detector is placed horizontally while the polarization is vertical, in which case there is a 50-50 chance of getting a green light. This just means that if we do the experiment with this last alignment 100 times, about 50 of them we will get a green light and about 50 of them red (This is just probabilities however; we may as well get 100 times the same light in actuality).
Now let’s calculate again the probability that both detectors will flash green under this new Quantum view. For simplification let’s assume that the axes that the detectors can be aligned are 120 degrees apart.
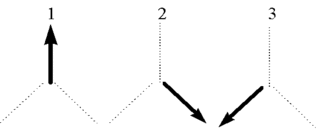
Suppose we align detector A along direction 1. When the photon is detected, let’s assume it generates a green light. According to what we said in assumption 2, we instantly know now that the other photon is also pointing along direction 1. So, what is the probability that the other detector will also flash green?
Well, the detector will either be pointing along direction 1, or direction 2, or direction 3. If it is pointing along direction 1 it will flash green with probability cos^2(0)=1. If it is pointing along direction 2 it will flash green with probability cos^2(-120)=1/4, and if it is pointing along direction 3 it will flash green with probability cos^2(120)=1/4. Hence the total probability is
P = (1 + 1/4 + 1/4)/3 = 1/2
In this case we see that if Quantum Mechanics is right, Bell’s inequality is violated since it says that this probability should be always greater than 5/9 > 1/2 .
Why is this result different than the common-sense answer 5/9? Because we allow for instant communication between the 2 photons, so that when the first is measured the other is instantly aligned in the same direction.
Note that if you only measured instead of 3 directions just 2 (say up and down) there is no violation of the inequality (in that case Bell says P>=1/2 and QM says P=1/2 - try it). The difference is that with 2 measurement directions we know beforehand what the other detector will flash. If the first detector flashes green, the other will flash green too. If it flashes red, the other will flash red too. However with 3 measurement directions even if the first detector flashes green the second detector still has a chance of flashing red.
Before making any measurement, we predict that the probability is 5/9. After doing the measurement, the probability drops to 1/2. The action of measuring affects the probabilities of the outcomes - that concept lies at the heart of this story and transcends Quantum Mechanics.
Concluding, all these are just predictions until they are tested by experiment. In 1983 Alain Aspect did the first thorough experiment and proved that Bell’s inequality was violated by 5 standard deviations. However Bell himself had pointed out that ideally the detectors had to be separated far away, so that there is no way for a signal to travel between them.
Otherwise maybe after you set the detector’s direction there can be a way for the photons to have predetermined at birth polarization and still get the violation answers (for example, if the detectors somehow communicate with each other). To prove the instant action from a distance, you have to have the detectors far far away.
In 1998 at team at Innsbruck generated 2 photons, fed them into optical fibers and sent them 400m apart allowing for 1.6 μs of time to decide for the orientation of the detectors after any light speed signal could travel between them. Then they sat down in their computers and waited to observe a posteriori the data from the detectors.
Low and behold, each time they changed the orientation of the detectors they saw a change in the statistics - that somehow the photons where communicating instantly when measured. Or better, that they are a single entity and not 2 individual items. The experiment violated the inequality with unprecedented accuracy. The paper was published in Nature the next year and Alain Aspect reviewed it.
I will end the story by quoting Aspect who mostly quotes Feynman at the last paragraph of his review:
It has not yet become obvious to me that there is no real problem… I have entertained myself always by squeezing the difficulty of Quantum Mechanics into a smaller and smaller place, so as to get more and more worried about >that particular item. It seems almost ridiculous that you can squeeze it to a numerical question that one thing is bigger than the another. But there you are - it is bigger…
Yes, it is bigger by 30 standard deviations.
Thanks to Gary Felder and his excellent article on Bell’s theorem.
