Side Projects / Plasma Wakefield Acceleration

Between 2003 and 2008 I worked on my PhD, my research focusing on plasma-based particle accelerators. It deals with the utilization of electric fields excited in plasmas (ionized gases) in order to accelerate charged particles into high energies. This is presently done using conventional techniques available in accelerators such as the LHC, however such schemes have reached close to their upper theoretical limit and cannot be extented further. Plasma-based accelerators are presently the best bet for the next generation of machines.

My work focused on the use of multiple electron bunches in order to excite fields in plasmas in an efficient way with potential applications to future particle colliders. You can navigate through some of the main results below. The relevant references are provided along the way. For the full details check my dissertation [pdf].

1. INTRODUCTION TO PLASMA-BASED ACCELERATION

Particle Accelerators

We are trying to prove ourselves wrong as quickly as possible, because only in that way can we find progress.

Richard Feynman

This is how the celebrated physicist Richard Feynman described the evolution of physics in his famous series of lectures he gave at Cornell University in 1965 regarding the character of physical laws. Indeed, the experimenters are not very interested in confirming already-established laws under regular conditions. Rather, they prefer to look carefully in those places where the laws are most likely to be falsified. Consider for example the experiments that measured the blackbody spectrum and the bending of light near the sun in the early 20th century which challenged our understanding of nature, thus allowing Max Planck and Albert Einstein, respectively, to suggest that energy is quantized and that space is not flat , ultimately giving birth to the modern theories of Quantum Mechanics and General Relativity.

Today and for the past 70 or so years, the most successful tools that we use to look into those new regimes are particle accelerators. These machines use strong electric fields to accelerate charged particles such as electrons and protons to high energies which are then smashed against each other at near the speed of light. By observing the behavior of the products of those collisions, the elementary constituents of matter can be analyzed and new fundamental laws can be formed. The ongoing success of these colliders has relied on the technological developments that allow them to accelerate particles at ever higher energies: From Einstein’s famous mass-energy equivalence equation, higher energies translate to more massive particles that can be created and detected in the accelerators.

The energy of accelerators has increased almost 10 orders of magnitude since the first cyclotrons where constructed in the early 1930s, and this scaling has produced some amazing discoveries in the field of particle physics as the higher energies allowed for heavier particles to be detected. Most of the quark structure inside protons and neutrons was identified in the 1970s and 1980s at the Stanford Linear Accelerator Center (SLAC), with masses that range between 1 MeV/c2 (for the up quark) to 5 GeV/c2 (for the bottom quark). The carriers of the electroweak force, W and Z bosons, were discovered in 1983 at CERN’s Super Proton Synchrotron (SPS) and were found to have masses 80 GeV/c2 and 90 GeV/c2, respectively. The heaviest elementary particle known to date, the top quark, was discovered only in 1995 at Fermilab’s Tevatron accelerator with a mass of 171 GeV/c2. Without particle accelerators, our understanding of the four fundamental forces of nature would have been limited to Einstein’s theory of gravity from 1915 and Maxwell’s equations for electromagnetism from 1865.

This success though has not happened without cost, as accelerators have come a long way since Lawrence’s first 1 MeV cyclotron in 1932 which was a mere 10 cm long. The price, complexity and size of the latest particle accelerators have skyrocketed along with their energy. This dissertation is written in 2008, the year that the Large Hadron Collider (LHC) is commissioned. The LHC is the largest and most complicated machine ever constructed by humans, a circular 14 TeV proton – proton collider built underground in a 27 km tunnel at CERN, near the French-Swiss borders. This worldwide effort of 2,000 scientists from 34 countries will look for, among other things, the Higgs Boson with an upper expected mass of 144 GeV/c2 (which may provide the tools to unify the three of the four fundamental forces), evidence for supersymmetric particles (which may explain the excess of non-baryonic matter in the universe) and string theory’s extra dimensions (which may explain why gravity is so weak compared to the other forces in nature). The price tag for LHC is between $5 – 10 billion.

LHC – scale accelerators are very close to the limit of what we can practically afford to build using conventional technologies, even collaboratively. The International Linear Collider (ILC), a proposed 1 TeV lepton smasher, is estimated to cost $7 billion and extend over 30 km in length, more than 10 times the length of SLAC. The Compact Linear Collider (CLIC) is another scenario of a proposed lepton collider at 3 TeV with a length of 33 km and similar cost. Any such projects will be extremely hard to finance and may ultimately follow the path of the Superconducting Super Collider (SSC), a 87 km circumference accelerator that was cancelled after the projected cost exceeded $12 billion in 1993.

The reason why the cost has been scaling with the collider energy is that the accelerating gradients (i.e., the energy gained per unit length) have more or less remained constant over the past few decades, in the order of 10 – 100 MV/m. Therefore, the only way to scale into higher energies is to simply make the accelerating portion longer, thus increasing the construction and maintenance costs at the same time. Those conventional techniques rely on radio-frequency electric fields that propagate inside metallic cavities. One of the major limitations of this technology is that if the accelerating fields are increased beyond a certain point, the modules are damaged because the energy from these fields is approaching the energy that binds electrons to the atoms in the cavity walls and tears them apart. This is why the ILC gradient can only be 40 MV/m (limited by the loss of superconductivity in the niobium cavities due to heat), only two times larger than the 20 MV/m of the 40 year old SLAC. Clearly, a revolution is needed here; a new acceleration technology that will do for the accelerators what the transistor did for the electronics 60 years ago: miniaturize them.

Plasma-based Acceleration

The new particle acceleration technology that is the subject here is plasma accelerators. The main principle behind it is that one can use a relativistic electron beam (Plasma Wakefield Acceleration – PWFA) or a laser pulse (Laser Wakefield Acceleration – LWFA) to excite relativistically moving waves in plasmas (ionized gases). The electric fields excited in those waves are at least 2 – 3 orders of magnitude stronger than the ones supported by the conventional metallic cavities, and thus, when utilized properly, they are used to accelerate particles to high energies in much smaller distances (thus reducing the cost). In addition, since plasma accelerating cavities (which are created dynamically every time) consist of already ionized particles, they do not suffer from the material breakdown damage like the conventional metallic cavities.

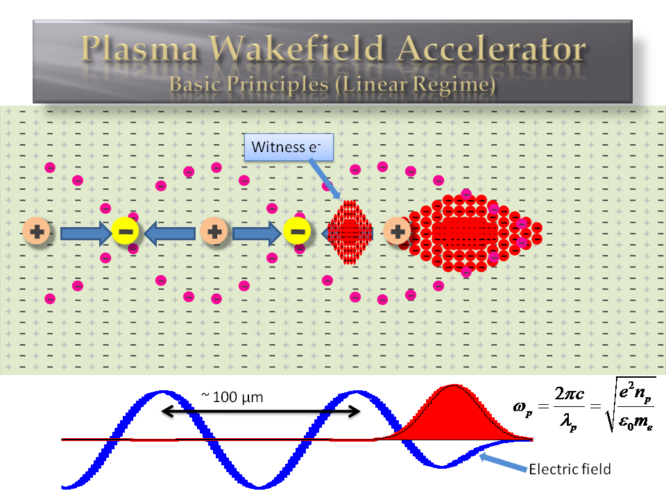
As the relativistic electron beam or the laser beam propagates inside the plasma, the electric field of the beam displaces the plasma electrons, while the plasma ions are much heavier and stay static. Eventually the electrons are drawn back on the axis from the force of the positively charged ions, overshoot the axis, and they start to oscillate (perpendicular to the propagation direction of the beam in this figure). This sets up a charge density wave behind the beam, since the regions where the electrons cross the axis are more negatively charged than the regions where the electrons are far away from the axis. This charge difference creates a very strong electric field that propagates at the velocity of the beam. As a result, if a witness electron beam is placed at the proper phase, it will experience this accelerating field and be propelled to high energies.

The physical reason why plasmas can support those high gradients is the collective effect of the plasma electrons. As opposed to the other three states of matter where the particles and molecules are distributed in a fuzzy and incoherent way, inside a plasma its billions of freed electrons can be manipulated together and forced to act coherently. The success of the future plasma accelerator will rely on maintaining this nice collective behavior over long enough distances. Moreover, it should be pointed out that the plasma accelerator is merely an energy transformer. It does not provide energy; it may only transfer the energy of an existing beam to a trailing beam. As such, it still requires a pre-created driver to provide the initial energy to be extracted. Therefore, the plasma accelerator will not replace existing accelerators; it will rather extend them to higher energies.

2. ACCELERATION OF A TRAILING BUNCH (2-BUNCH EXPERIMENTS)

This set of experiments tackled the problem of accelerating a trailing electron bunch in the wakefield excited by a preceding bunch. While the first ever plasma wakefield experiment was a two-bunch experiment like that, the gradients were extremely low (~4 MeV/m) and the results were not direct - they required complex mathematical extrapolations in order to make sense of the data. Our results performed at the Accelerator Test Facility of the Brookhaven National Laboratory improved the previous measured gradient by two orders of magnitude and provided clean, direct measurements of the energy exchanges between the electron bunches. Meanwhile, more recent PWFA experiments at SLAC did demonstrate ultrahigh gradients (50 GeV/m) but there weren’t many accelerated electrons because a single bunch was used both to excite the waves (head) and measure the energy exchange (tail).

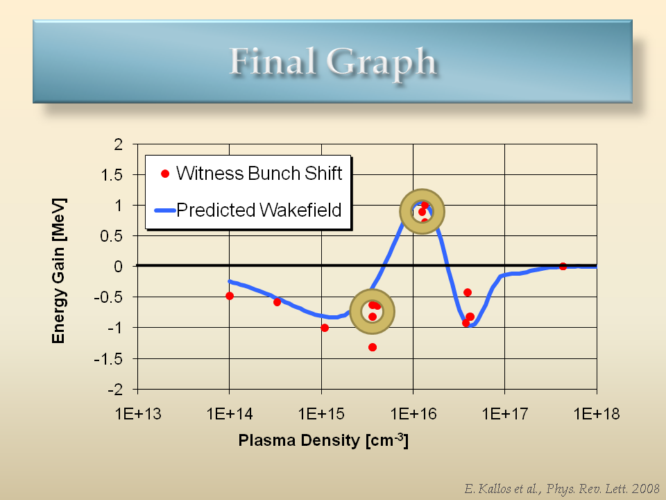
Two electron bunched were fed into a 6-mm long plasma, with a constant distance between them. The idea is that the first bunch would excite the wave, and then we would observe the energy shifts of the trailing, smaller bunch, as the plasma density was varied (and thus the plasma wavelength, altering the effective position between the bunches). The above graph shows the energy shifts of the trailing bunch as a function of the plasma density. To illustrate the physics of the interaction, we will observe more closely the two data points that are encircled.

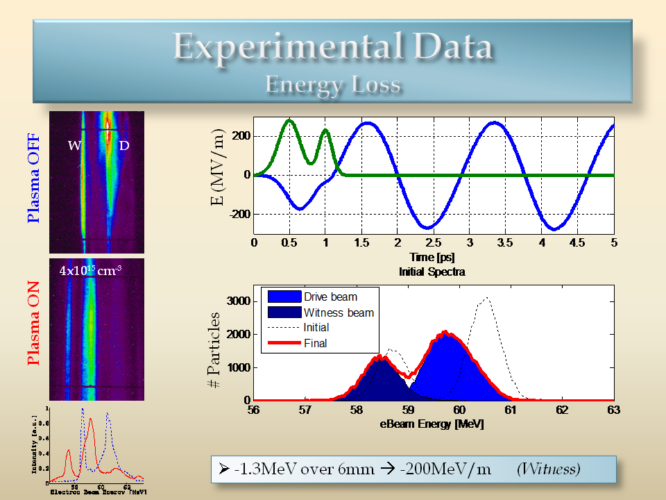
At a density of 4e15, the plasma wavelength is long enough to cover both bunches. Thus, both bunches drive the wakefield producing an equivalent average energy gradient over the 6 mm capillary length of 200 MeV/m. The bunches shift towards lower energy, as also indicated by the simulated spectrum.

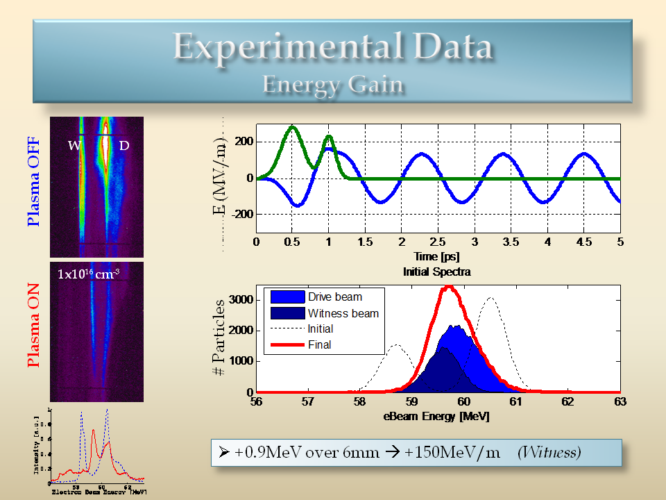
When the density was raised to 1e16, we experimentally observe that the witness bunch now shifts towards higher energies. This is interpreted through the simulation: the wavelength is now smaller, and while the first bunch deposits its energy, the second bunch is absorbing that energy, and thus it accelerates. Over the distance of 6 mm, the bunches happen to lose and gain energy respectively such that they overlap in the energy spectrum, producing the energy peak observed in the center of the spectrum. The total, loaded energy gradient observed was 150 MeV/m.

The main paper discussing the results is [1], while [2] and [3] provide further information on the details of setting up the experiment.

[1] High-gradient Plasma Wakefield Acceleration with two subpicosecond electron bunches
Efthymios Kallos, Tom Katsouleas, Wayne D. Kimura, Patric Muggli, Igor Pavlishin, Igor Pogorelsky, Daniil Stolyarov, Vitaly Yakimenko
Phys. Rev. Lett. 100, 074802 (2008)

[2] Plasma Wakefield Acceleration Experiments Using Two Subpicosecond Electron Bunches
Patric Muggli, Wayne D. Kimura, Efthymios Kallos, Tom Katsouleas, Karl Kusche, Igor Pavlishin, Igor Pogorelsky, Vitaly Yakimenko
Proceedings of the 2007 IEEE Particle Accelerator Conference, Albuquerque, NM, pp.3079-3081 (2007)

[3] Subpicosecond Double Electron Bunch Generation
Wayne D. Kimura, Vitaly Yakimenko, Marcus Babzien, Xiaoping Ding, Eftymios Kallos, Tom Katsouleas, Karl Kusche, Patric Muggli, Igor Pavlishin, Igor Pogorelsky, Daniil Stolyarov, and Feng Zhou
Proceedings of the 12th Advanced Accelerator Concepts Workshop, Lake Geneva, WI, AIP Conference Proceedings No.877, pp.527-533 (2006)

3. EFFICIENT ACCELERATION AND MULTIBUNCH GENERATION (5-BUNCH EXPERIMENTS)

It is of great interest to create multiple bunches to excite the plasma waves. FIrst, because the maximum possible wakefield can be excited by the superposition of plasma waves excited by individual bunches, as shown below.

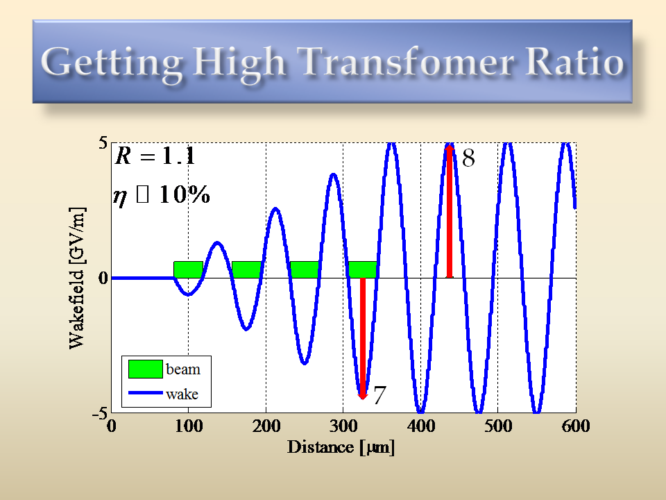
In this example 4 identical bunches excite the wakefield. The total wakefield amplitude is 4 times the amplitude of a single bunch. Thus, the gradient can be increased dramatically by adding more bunches. This is in the linear regime examined here, where the wake is simply proportional to the total charge fed into the plasma. The bunches must be separated by one plasma wavelength apart. On the other side, this scheme is very inefficient because the last bunch decelerates much faster compared to the early bunches, and only 10% of the initial energy of the bunches has been deposited to the plasma before that bunch has lost all its own energy.

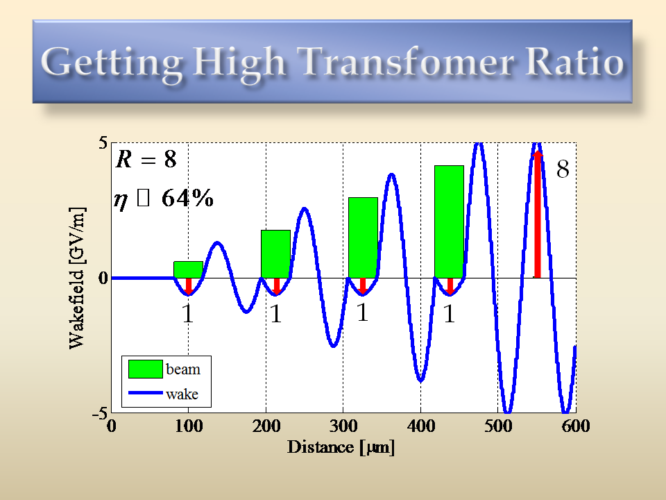
In a slightly different setup, the four bunches are placed 1.5 plasma wavelength apart, in effect each bunch absorbs some energy from the plasma instead of damping its own. At the same time, the charge per bunch is increased linearly to compensate for the increased wakefield due to more charge. As a result, each bunch now decelerates at the same rate (experience the same wakefield). In the case above 16 times more charge than a single bunch is fed into the plasma, and the final wake increases only 8 times (instead of the maximum possible of 16), but now the efficiency is 64% (limited by the wake variation under each bunch), thus more energy is damped into the plasma, and more energy could be transferred to a later trailing bunch. This scheme thus allows the accelerator to run over longer distances.

For more details on these schemes, see references [4] and [5].

[4] Simulations of a High-Transformer-Ratio Plasma Wakefield Accelerator Using Multiple Electron Bunches Efthymios Kallos, Patric Muggli, Tom Katsouleas, Vitaly Yakimenko, Jangho Park and Karl Kusche
Proceedings of the 13th Advanced Accelerator Concepts Workshop, Santa Cruz, CA, Vol.1086, pp.580-585 (2008)

[5] Plasma Wakefield Acceleration Utilizing Multiple Electron Bunches
Efthymios Kallos, Tom Katsouleas, Patric Muggli, Igor Pavlishin, Igor Pogorelsky, Daniil Stolyarov, Vitaly Yakimenko, Wayne D. Kimura
Proceedings of the 2007 IEEE Particle Accelerator Conference, Albuquerque, NM, pp.3070-3072 (2007)

Thus, is it of great interest to examine these schemes and the properties of multibunch acceleration, as high efficiency is the ultimate goal of any particle accelerator.

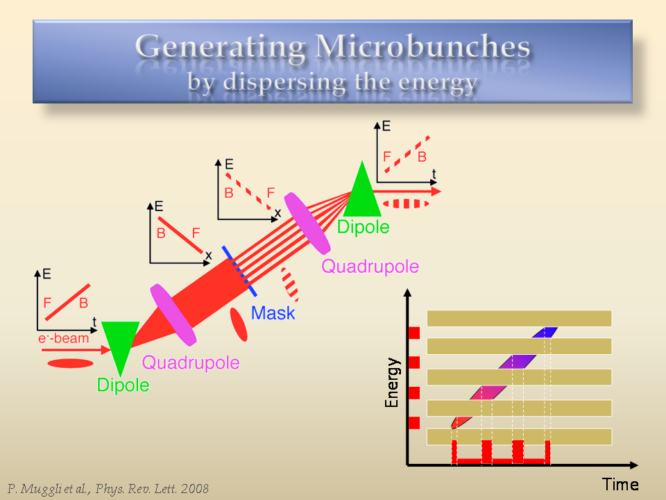
In order to create such bunches, we used a mask technique, shown above. A single electron beam is dispersed in energy, and then spread through a magnetic dipole. Thus, the energy-time correlation becomes an energy-space correlation. At the dispersion plane, a metal mask is placed, consisting of simple metal wires that block some portions of the initial beam. What is left is inversely dispersed and brought back to an energy-time correlation, creating multiple bunches in time.

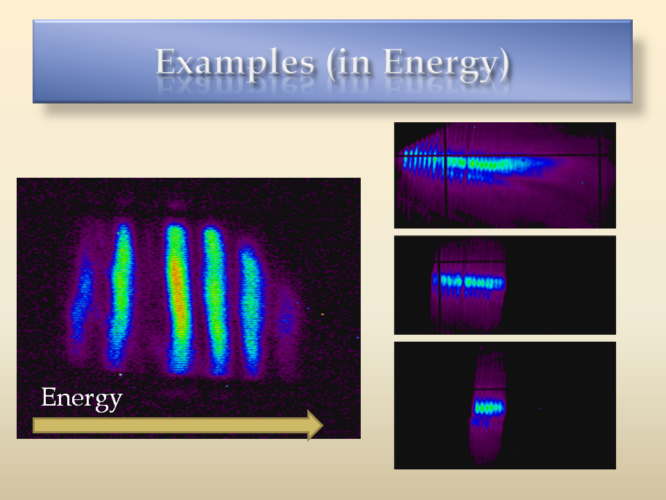
An example of how the bunches look in energy is shown above. By adjusting a slit, the number of bunches transmitted can be controlled.

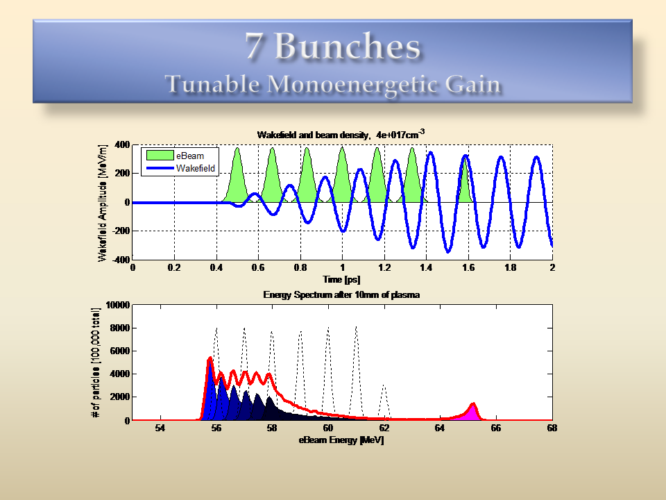
Here are some simulations of what can be done with such bunches. Measuring the maximum possible wakefield by having equidistantly spaced bunches is the simplest first step to demonstrate that superposition in plasma waves can work. In the example above, 7 bunches excite a high wake, and a last witness bunch can sample the wake and be accelerated. The details of this technique can be found in [6].

[6] Generation of Trains of Electron Microbunches with Sub-picosecond Spacing
Patric Muggli, Vitaly Yakimenko, Wayne D. Kimura, Marcus Babzien, Efthymios Kallos and Karl Kusche
Phys. Rev. Lett. 101, 054801 (2008)

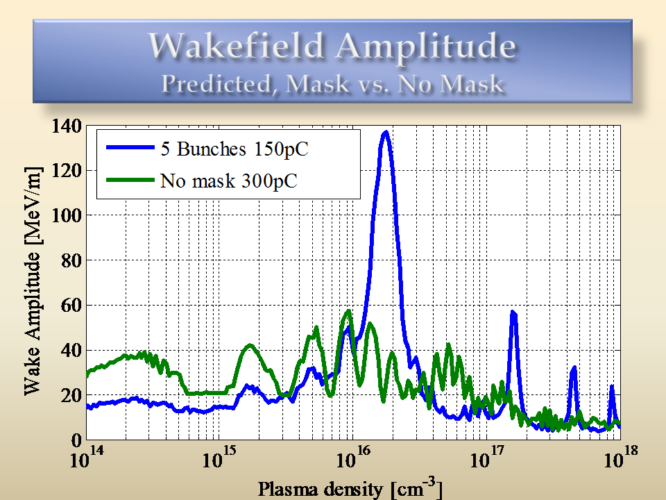
This is a prediction for the wake as a function of plasma density, for bunches that can be created at ATF using this technique. A 300 pC beam creates a maximum wake of 60 MeV/m, that varies slowly with density. When portions of the beam are blocked, and only 150 pC of charge is allowed through in 5 bunches, the wake is generally lower, except for the region where the bunches are in resonance with the plasma wave. Then the wake amplitude is almost doubled, even though the total charge fed in half. The width of the resonance is inversely proportional to the number of bunches used (in this case roughly 1/5=20%).

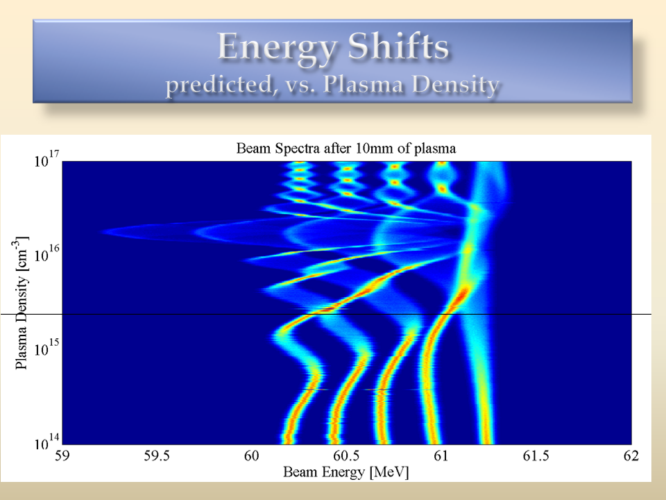
Here the figure shows how the energy spectrum recorded would look like as a function of plasma density for the 5 drive bunches mentioned earlier. There is clearly a region where the resonant effect can be detected. This is running 5 experiments at once: the right-most bunch (higher energy) is first and only sees its own wake, thus graphing a single curve. The second bunch from the right sees its own wake and the wake of the first bunch, thus the dip at some specific energy. This is essentially the same graph as shown in the previous section for the double bunch experiment. The later bunches are shifting accordingly.

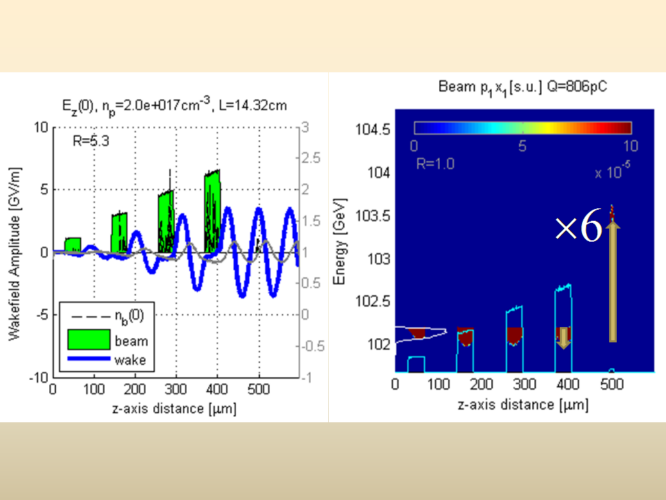
Ultimately, for use in a future high-energy collider, the maximum efficiency scheme will be utilized. The figure above shows a simulation in OSIRIS where 4 ramped drive bunches and a witness bunch are fed into a high-density plasma. After 45 cm of propagation in the plasma, the 4 drive bunches have lost roughly the same energy, while the witness bunch has gained roughly 6 times the energy each other bunch has lost into the plasma. A 3 GeV/m gradient is maintained here over that plasma length, however it is challenging to sustain this over meter-long distances due to the non-linear focusing forces that appear in the linear regime of PWFA.

4. RESONANT WAKEFIELD EXCITATION (100-BUNCH EXPERIMENTS)

The following idea is the answer to the question: given a fixed amount of charge, what it the maximum possible wakefield that can be excited in a plasma?

Answer: Since the plasma is an oscillator, the maximum excitation of any harmonic system is to excite it with a periodic driver (i.e. delta functions), with period equal to the resonant frequency of the system.

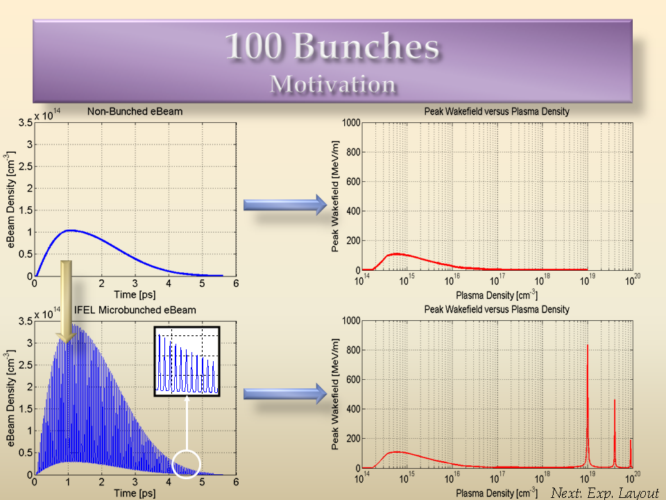
Here, the initial electron beam is modulated into a series of very short bunches, spaced at the plasma wavelength. The total charge remains the same.The unbunched beam creates a small response, but the modulated beam creates one order of magnitude stronger response at the frequency of oscillation.

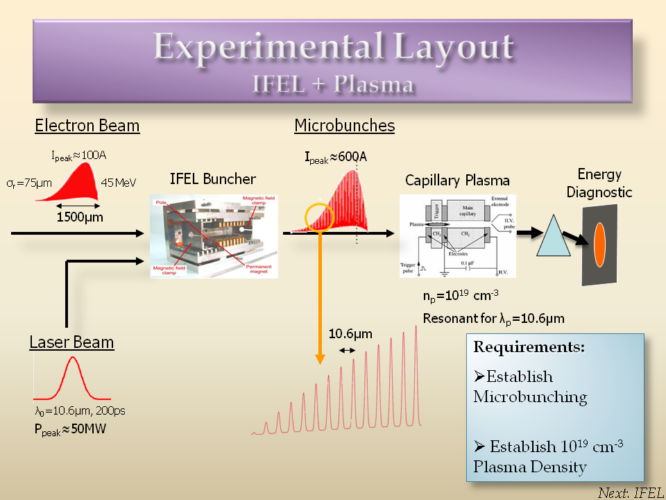
For the experiments designed for ATF, the beam can be modulated using a CO2 laser through a process called IFEL (see reference [7]). Thus, the maximum wake would be obtained with a plasma at a frequency (or density) exactly at the laser’s wavelength, 10.6 μm.

[7] Plasma-Based Advanced Accelerators at the Brookhaven Accelerator Test Facility I. V. Pogorelsky, M. Babzien, K. P. Kusche, I. V. Pavlishin, V. Yakimenko, C. E. Dilley, S. C. Gottschalk, W. D. Kimura, T. Katsouleas, P. Muggli, E. Kallos, L. C. Steinhauer, A. Zigler, N. Andreev, D. B. Cline and F. Zhou
Laser Physics, Vol.16, No.2, pp. 259-266 (2006)

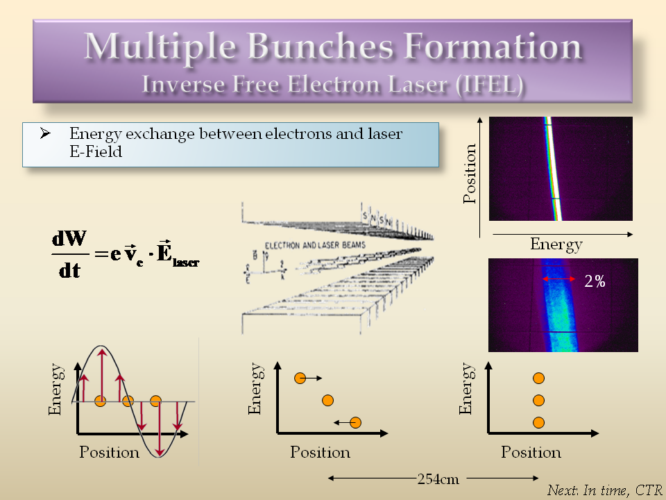
In the IFEL, the electron and laser beams co-propagate inside a static magnet (wiggler). The energy spread shown in the spectrometer corresponds to accelerated and decelerated particles. When left to propagate in free space after the wiggler, the catch up together forming microbunches, roughly ~1 μm wide.

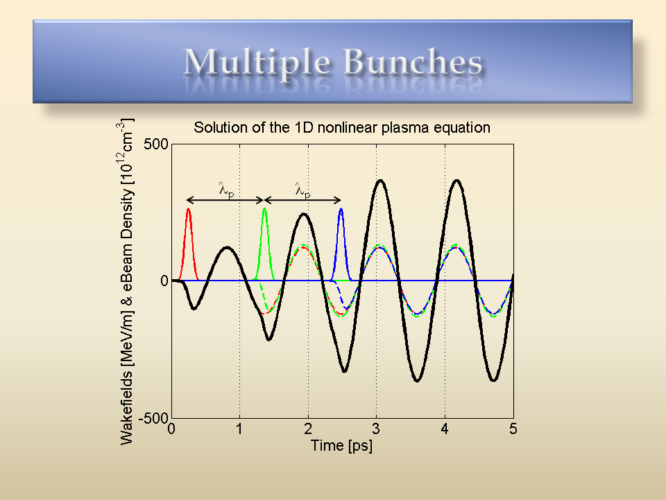
The main principle of multibunching: short bunches separated by one plasma wavelength apart, resonantly drive a wakefield in the plasma through superposition of their individual wakes.

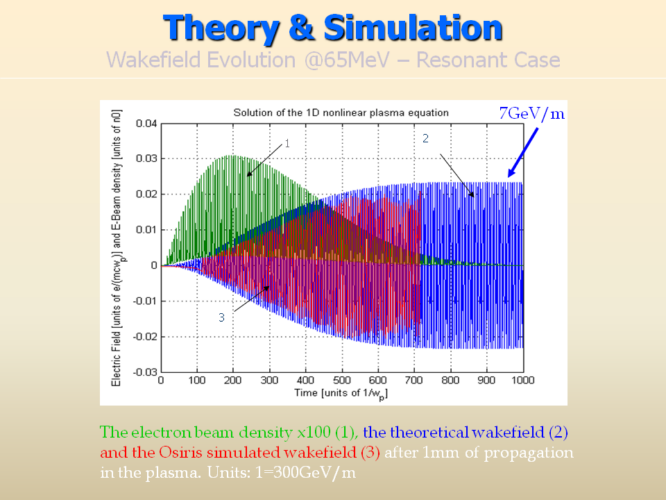
The above graph shows an OSIRIS simulation when a multibunched electron beam is fed into the plasma. A very large wake amplitude can be obtained. The simulation agrees well with the theory in this case, as everything is still in the linear regime. For more details, see [8] and [9].

[8] A Multibunch Plasma Wakefield Accelerator
Efthymios Kallos, Tom Katsouleas, Patric Muggli, Ilan-Ben Zvi, Igor Pogorelsky, Vitaly Yakimenko, Igor Pavlishin, Karl Kusche, Marcus Babzien, Feng Zhou and Wayne D. Kimura
Proceedings of the 2005 IEEE Particle Accelerator Conference, Knoxville, TN, pp.3384-3386 (2005)

[9] Plasma Simulations and Multibunched Electron Beam Diagnostics
Efthymios Kallos, Patric Muggli, Tom Katsouleas, Vitaly Yakimenko, Daniil Stolyarov, Igor Pogorelsky, Igor Pavlishin, Karl Kusche, Marcus Babzien, Ilan Ben-Zvi and Wayne D. Kimura
Proceedings of the 12th Advanced Accelerator Concepts Workshop, Lake Geneva, WI, AIP Conference Proceedings No.877, pp.520-526 (2006)

5. PLASMA DIAGNOSTICS

Obviously all the experiments mentioned until now could not be done without a good knowledge of the plasma density. We developed a number of diagnostics to measure the density and temperature of the plasma, as well as designed novel plasma sources.

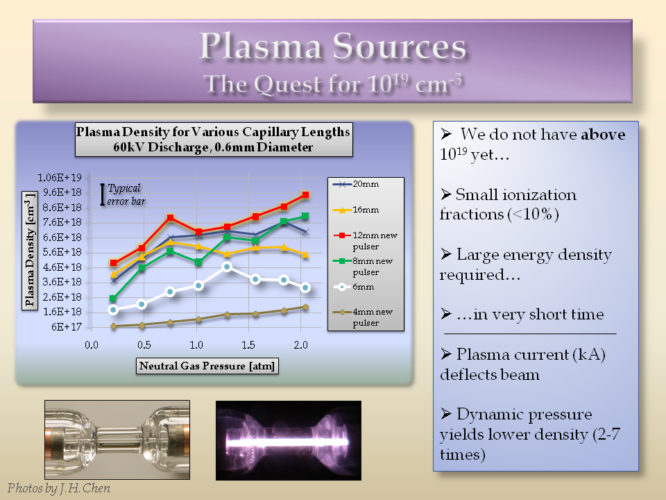
In a typical example, a small glass tube 10 cm long by 0.5 mm wide is fed with hydrogen gas, usually in the 0-2 atm range. By applying a high-voltage pulse, the gas breaks down creating the plasma for a short time. By collecting the light emitted and analyzing its spectrum, the density is measured through Stark Broadening. The desired density can be tuned by adjusting the capillary geometry, the gas pressure or the initial pulse. There are also less reliable ablative capillaries where the plasma is formed by the strong current evaporating the capillary walls. For more details on the capillary measurements, see [10].

[10] A High Density Hydrogen-Based Capillary Plasma Source for Particle-Beam-Driven Wakefield Accelerator Applications
Hao Chen, Efthymios Kallos, Patric Muggli, Thomas C. Katsouleas and Martin A. Gundersen
IEEE Transactions on Plasma Science, Vol.37, No.3, pp.456-562 (2009)

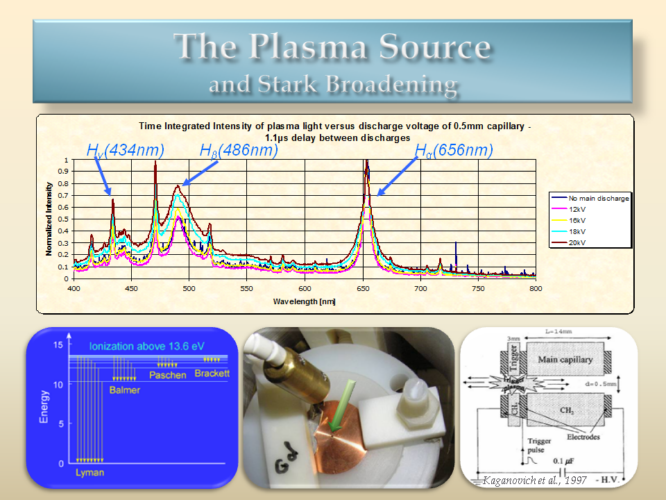
The diagnostic itself, mainly Stark Broadening, is based on electronic transitions inside the atoms. We mostly measured the balmer lines which correspond to the visible spectrum, which are transitions inside the hydrogen atom from higher levels down to the n=2 level of the atom. The width of the light emitted in those specific frequencies are correlated to the density and temperature of the plasma through theory developed by Griem.

6. ELECTRON BEAM DIAGNOSTICS

Especially for multibunch experiments, it is also a great deal important to measure the characteristics of the electron beams produced.

In the two-bunch experiment, a simple interferometer was used. A foil was insterted in the path of the beam, which emits CTR light. The light is interfered with itself to provide an auto-correlation signal from which the length of the bunches can be subsequently extracted. See [12] for details. A similar technique can be used to estimate the bunching of the multibunches, when 2-10 bunches are present into the beam, as detailed in [13].

[12] Subpicosecond Double Electron Bunch Generation
Wayne D. Kimura, Vitaly Yakimenko, Marcus Babzien, Xiaoping Ding, Eftymios Kallos, Tom Katsouleas, Karl Kusche, Patric Muggli, Igor Pavlishin, Igor Pogorelsky, Daniil Stolyarov, and Feng Zhou
Proceedings of the 12th Advanced Accelerator Concepts Workshop, Lake Geneva, WI, AIP Conference Proceedings No.877, pp.527-533 (2006)

[13] Generation and Characterization of the Microbunched Beams with a Mesh Target
Patric Muggli, Efthymios Kallos, Vitaly Yakimenko, Marcus Babzien, Karl Kusche, Wayne D. Kimura Proceedings of the 2007 IEEE Particle Accelerator Conference, Albuquerque, NM, pp.3073-3075 (2007)

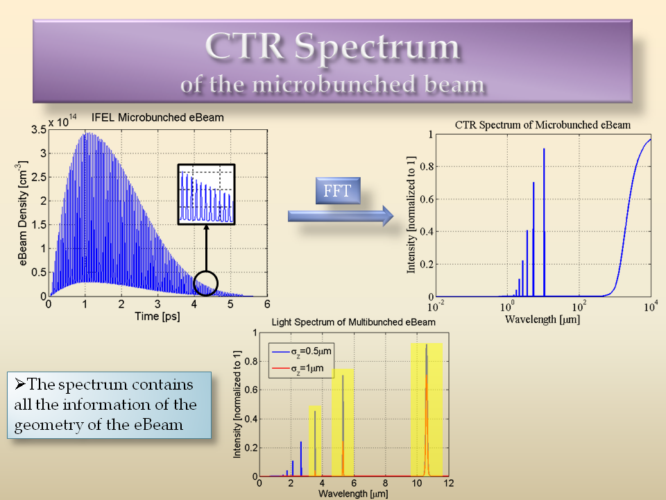
For the multibunch case we make use of the fact that the CTR spectrum is proportional to the Fourier Transform of the input beam profile. The bunching quality of the beam is thus directly mapped into the harmonics of the spectrum at each frequency. By measuring the light emitted at specific wavelengths, their ratio provides indication for the distance between the microbunches. See [14] for details.

[14] Plasma Simulations and Multibunched Electron Beam Diagnostics
Efthymios Kallos, Patric Muggli, Tom Katsouleas, Vitaly Yakimenko, Daniil Stolyarov, Igor Pogorelsky, Igor Pavlishin, Karl Kusche, Marcus Babzien, Ilan Ben-Zvi and Wayne D. Kimura
Proceedings of the 12th Advanced Accelerator Concepts Workshop, Lake Geneva, WI, AIP Conference Proceedings No.877, pp.520-526 (2006)

BONUS MATERIAL

During the 5-year-long Ph.D. a lot of things happened. Here are a couple of fun slides that I presented in a few special cases.

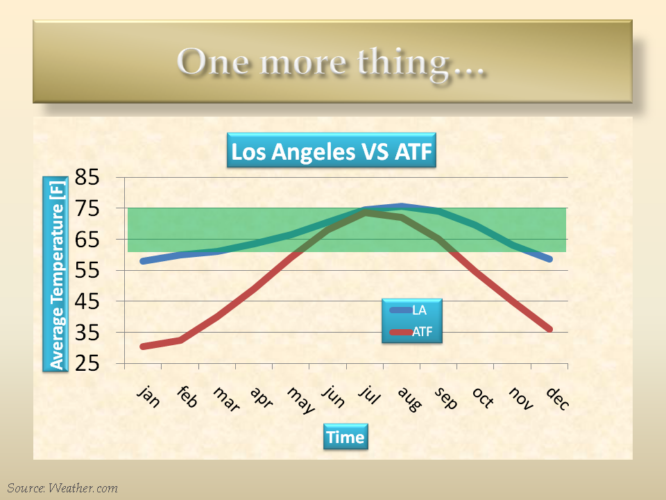
At ATF, where we spent most of the time doing experimental work, the climate is not exactly ideal. See how ATF’s temperature is barely in the comfort zone for only a couple of months, and way outside it the rest of the year. The comparisons with Los Angeles are futile!